Algoritma hazırlanırken, çözüm için yapılması gerekli işlemler, öncelik sıraları göz önünde bulundurularak ayrıntılı bir biçimde tanımlanmalıdırlar. Yazılan komutun tek bir anlama gelmesi ve herkes tarafından anlaşılır olması gereklidir. Yazılan komutların uygulanabilir olması gereklidir. Her algoritmanın sonlanması, çalıştırılan komut sayısının sonsuz olmaması gereklidir.
Verilen bir problemin bilgisayar ortamında çözülecek biçimde adım adım ortaya koyulması ve herhangi bir programlama aracıyla kodlanması sürecidir. Çözüm için yapılması gereken işlemler hiçbir alternatif yoruma izin vermeksizin sözel olarak ifade edilir. Verilerin, bilgisayara hangi çevre biriminden girileceğinin, problemin nasıl çözüleceğinin, hangi basamaklardan geçirilerek sonuç alınacağının, sonucun nasıl ve nereye yazılacağının sözel olarak ifade edilmesi biçiminde de tanımlanabilir.
Algoritma Süreci
1- Tasarım (design)
2- Doğruluğunu ispat etme (validation)
3- Analiz (analysis)
4- Uygulama (implementation)
5- Test
Kaba‐Kod (Pseudo Code)
Kaba‐kod, bir algoritmanın yarı programlama kuralı, yarı konuşma diline dönük olarak ortaya koyulması, tanımlanması, ifade edilmesidir. Kaba‐kod, çoğunlukla, bir veri yapısına dayandırılmadan algoritmayı genel olarak tasarlamaya yardımcı olur.
Gerçek Kod
Algoritmanın herhangi bir programlama diliyle, belirli bir veri yapısı üzerinde gerçekleştirilmiş halidir. Bir algoritmanın gerçek kodu, yalnızca, tasarlandığı veri yapısı üzerinde çalışır. Bir algoritma kaba‐kod ile verilirse gerçek kod verilmesinden daha kolay anlaşılır.
Kaba‐kod: temel gösterim
1. Bir değer atamak için genellikle:= kullanılır. = işareti ise eşitlik kontrolü için kullanılır.
2. Metot, fonksiyon, yordam isimleri: Algoritma Adı ({parametre listesi})
3. Program yapısı şu şekilde tanımlanır:
•Karar yapıları: if … then … else …
•while döngüleri: while … do {döngü gövdesi}
•Tekrar döngüleri: repeat {döngü gövdesi} until …
•for döngüleri: for … do {döngü gövdesi}
•Dizi indeksleri: A[i]
4. Metotların çağrılması: Metot adı ({değişken listesi})
5. Metotlardan geri dönüş: return değer
Algoritmaların kaba‐kod olarak ifade edilmesi
Örnek: Bir dizideki elemanların toplam ve çarpımını hesaplayan algoritmayı kaba‐kod kullanarak tanımlayınız.
Toplam Ve Çarpım Hesapla (dizi, toplam, çarpım)
Girdi: n sayıdan oluşan dizi.
Çıktı: dizi elemanlarının toplam ve çarpım sonucu
for i:= 1 to n do
toplam:= toplam + dizi[i] toplam: toplam + dizi[i]
çarpım:= çarpım* dizi[i]
endfor
Kaba‐kod ve Gerçek Kod
Algoritma Analizi
Algoritma analizi, tasarlanan program veya fonksiyonun belirli bir işleme göre matematiksel ifadesini bulmaya dayanır. Burada temel hesap birimi seçilir ve programın görevini yerine getirebilmesi için bu işlemden kaç adet yapılması gerektiğini bulmaya yarayan bir bağıntı hesaplanır. Eğer bu bağıntı zamanla ilgiliyle çalışma hızını, bellek gereksinimiyle ilgiliyse bellek gereksinimi ortaya koyar.
Neden algoritmayı analiz ederiz?
Algoritmanın performansını ölçmek için. Farklı algoritmalarla karşılaştırmak için Daha iyisi mümkün mü? Olabileceklerin en iyisi mi?
Algoritmayı nasıl analiz ederiz?
Yürütme zamanı(Running Time)-T(n)
Karmaşıklık (Complexity) -Notasyonlar
Yürütme Zamanı; Bir programın veya algoritmanın işlevini yerine getirebilmesi için, temel kabul edilen işlevlerden kaç adet yürütülmesini veren bir bağıntıdır ve T(n) ile gösterilir.Temel hesap birimi olarak, programlama dilindeki deyimler seçilebildiği gibi döngü sayısı, toplama işlemi sayısı, atama sayısı, dosyaya erişme sayısı gibi işler de temel hesap birimi olarak seçilebilir.
Algoritma 1, T1(N)=1000N
Algoritma 2, T2(N)=N2
| N | T1 | T2 |
| 10 | 10-2 sec | 10-4 sec |
| 100 | 10-1 sec | 10-2 sec |
| 1000 | 1 sec | 1 sec |
| 10000 | 10 sec | 100 sec |
| 100000 | 100 sec | 10000 sec |
N değerinin 1000’den küçük olduğu durumlarda iki algoritma arasındaki çalışma zamanı ihmal edilebilir büyüklüktedir.
Çalışma zamanının kesin olarak belirlenmesi zordur. Giriş verilerine bağlı olan en iyi durum (best case) Ortalama durum (average case); hesaplanması zordur. Diğerlerine göre en kötü durum (worst case); hesaplanması kolaydır. Bunun için çeşitli notasyonlardan faydalanılır.
Aritmetik Ortalama için T(n) Hesabı
Örnek 1: Aşağıda bir dizinin aritmetik ortalamasını bulan ve sonucu çağırana gönderen bulOrta() fonksiyonun kodu verilmiştir. Bu fonksiyonun yürütme zamanını gösteren T(n) bağıntısını ayrık C dili deyimlerine göre belirleyiniz.
float bulOrta(float A[], int n) {
{
float ortalama, toplam=0;
int k ;
1- for(k=0;k<n;k++)
2- toplam+=A[k];
3- ortalama=toplam/n
4- return ortalama;
}
Çözüm 1:
| Temel Hesap Birimi | Birim Zaman
(Unit Time) |
Frekans(Tekrar)
(Frequency) |
Toplam
(Total) |
|
| float bulOrta(float A[], int n) | – | – | – | |
| { | – | – | – | |
| float ortalama, toplam=0; | – | – | – | |
| int k ; | – | – | – | |
| 1- for(k=0;k<n;k++) | 1,1,1 | 1, (n+1), n | 2n+2 | |
| 2- toplam+=A[k]; | 1 | n | n | |
| 3- ortalama=toplam/n | 1 | 1 | 1 | |
| 4- return ortalama; | 1 | 1 | 1 | |
| } | – | – | – | |
| T(n)=3n+4 | ||||
Karmaşıklık (Copmlexity)
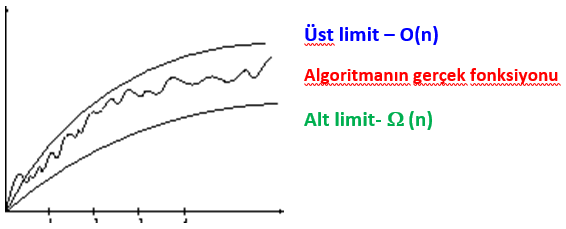
Karmaşıklık; bir algoritmanın çok sayıda parametre karşısındaki değişimini gösteren ifadelerdir. Çalışma (Yürütme) zamanını daha doğru bir şekilde bulmak için kullanılırlar. Genel olarak, az sayıda parametreler için karmaşıklıkla ilgilenilmez; eleman sayısı n‘nin sonsuza gitmesi durumunda algoritmanın maliyet hesabının davranışını görmek veya diğer benzer işleri yapan algoritmalarla karşılaştırmak için kullanılır. Karmaşıklığı ifade edebilmek için asimtotik ifadeler kullanılmaktadır. Bu amaçla O(n) (O notasyonu), W(n) (Omega notasyonu), θ(n) (Teta notasyonu) gibi tanımlamalara baş vurulur.
Strateji: Alt ve üst limitlerin bulunması
Algoritma Analizinde Bazı Kurallar
For Döngüsü: Bir For döngüsü için yürütme zamanı en çok For döngüsünün içindeki (test dahil) deyimlerin yinelenme sayısı kadardır.
İç içe döngüler (Nested Loops): İç içe döngülerde grubunun içindeki deyimin toplam yürütme zamanı, deyimlerin yürütme sürelerinin bütün For döngülerinin boyutlarının çarpımı kadardır. Bu durumda analiz içten dışa doğru yapılır.
For Döngüsü:
Ardışık deyimlerin toplam yürütme zamanını bulabilmek için sadece toplama yapılır.
Algoritma Analizinde Bir Örnek: İkili Arama Algoritması
İkili arama algoritması, sıralı dizilerde kullanılan bir arama metodur. Algoritma iteratif veya tekrarlamalı (recursive) olabilir. İterasyon ifadeleri (döngü) belirli bir koşul sağlanana kadar, verilen talimatların çalıştırılmasını sağlar.
Belirlenen koşul, “for” döngüsündeki gibi, önceden belirlenebilir veya “while-do” döngüsünde olduğu gibi net olarak belirlenmemiş, uçu açık da olabilir. Aşağıda iteratif olarak tasarlanmış ikili arama algoritmasına bir örnek verilmiştir.
Örnek : İkili Arama
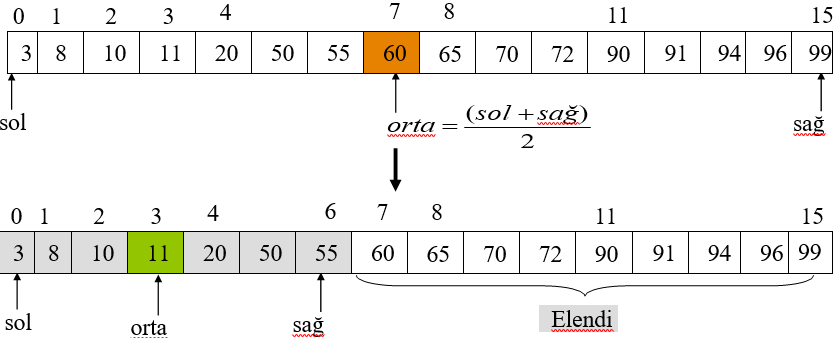
Dizi sıralanmış olduğundan, dizinin ortasında bulunan sayı ile aranan sayıyı karşılaştırarak arama boyutunu yarıya düşürülür ve bu şekilde devam edilir.
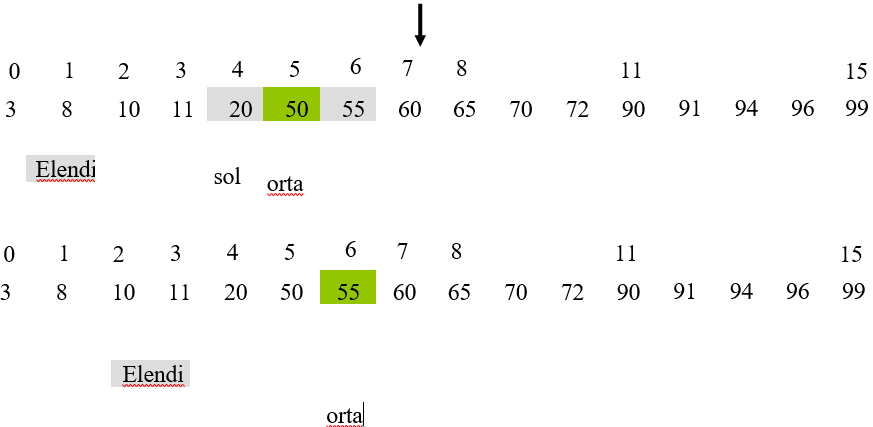
Örnek: 55’i arayalım
55’i bulduk ===> Başarılı arama şeklinde sonlanacak.
Hedefi ararken herhangi bir aşamada, arama alanımızı “sağ” ile “sol” arasındaki alana kısıtlamış oluyoruz.
“sol” ’un solunda kalan alan hedeften küçüktür ve bu alan arama alanından çıkarılır.
“sağ” ın sagında kalan alan hedeften büyüktür ve bu alan arama alanından çıkarılır.
İkili Arama – Algoritma
// Aranan sayının indeksini döndürür aranan sayı bulunamazsa -1 döndürür.
int ikiliArama(int A[], int N, int sayi){
sol = 0; sag = N-1;
while (sol <= sag){
int orta = (sol+sag)/2; // Test edilecek sayının indeksi
if (A[orta] == sayi) return orta; // Aranan sayı bulundu. İndeksi döndür
else if (sayi < A[orta]) sag = orta – 1; // Sağ tarafı ele
else sol = orta+1; // Sol tarafı ele
} //bitti-while
return –1; // Aranan sayı bulunamadı
} //bitti-ikiliArama
Kaynaklar;
Veri Yapıları ve Algoritmalar – Dr. Rifat ÇÖLKESEN, Papatya yayıncılık
Data Structures and Problem Solving Using Java – Mark Allen Weiss, Pearson International Edition
Veri Yapıları – Yrd.Doç.Dr. Erkan TANYILDIZI



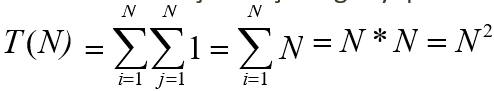
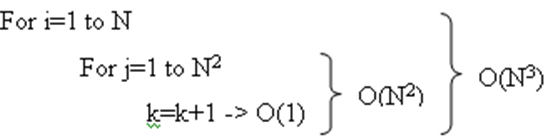
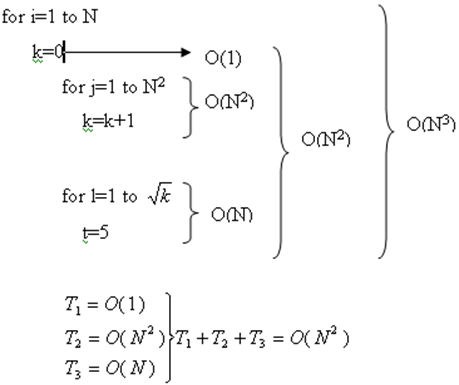







hocam yine güzel bir konu değinmişsiniz, veri yapıları ve algoritma dersinin vizesi için özet hazırlamama gerek kalmadı.
Genelde sınavlar için kısa ve öz yazmaya çalışıyorum. Size faydalı oldu ise ne mutlu bana.
ellerinize sağlık hocam emeğinizi taktir etmek gerek güzel bir paylasım olmus
Çok uzun ve geniş bilgiler vermişsiniz. Teşekkür ediyorum.
Değerli yorumunuz için ben teşekkür ederim.